tests d' aptitudes numériques
|
EPREUVES D'APTITUDE NUMERIQUE
|
|||||
| -REGLES GENERALES | |||||
| -Multiplication: Sachez le! Diviser un nombre par 10,100 ou mille equivaut a le multiplier par 0,1;0,01 ou 0,001 et vice versa diviser un nombre par; 0,1 revient a le multiplier par 10 le diviser par 0,01 équivaut a le multiplier par 100 etc... Exemple: 337 /1000 =337x0,001 =0,337 Exemple 22,12 / 0,001=22,12x1000=2212 | |||||
| -Multiplication et dividion par 5 , 25 et 125: Multiplier par 25 revient à diviser par 4 puis a multiplier par 100 : 25=100 / 4 Exemple: 48x25=48x100/4=48/4x100=12x100=120 | |||||
| -Multiplication par 11: | |||||
| -Les Fractions : a °n + a°p =a° n+p exemple:5°2+5°4=5°6 (°=puissance) a°n /a°p=a°n-p exemple: 5°2/5°4=1/5°2 | |||||
| -Identités
remarquables Les trois relations représentées ci-dessous sont les identités remarquables. Elles peuvent être utilisées dans de nombreux calculs algébriques. Précisons que le résultat de la première d’entre elle s’obtient avec la loi de la distributivité.    Exemples d’utilisation   |
|||||
|
Composantes d'une fraction La fraction a / b est composée d'un numérateur (a) et d'un dénominateur ( b). Fractions équivalentes Il est important de se rappeler qu'il existe plusieurs façons de représenter
la même fraction. Par exemple, les fractions 1/2 et 2/4 sont tout à fait
équivalentes.Mais comment passe-t-on d'une fraction à l'autre tout en
conservant la relation d'équivalence ? Une fraction reste équivalente si le numérateur
et le dénominateur sont multipliés ou divisés par le même nombre.
Exemple Exemple Simplification d'une fraction Une fraction est écrite sous forme simplifiée si le numérateur et le
dénominateur n'ont aucun facteur commun. En d'autres mots, sous forme
simplifiée, il est impossible de trouver un nombre qui soit diviseur à
la fois du numérateur et du dénominateur. Exemple La fraction 120 / 200 n'est pas écrite sous forme simplifiée puisqu'il
existe des nombres qui divisent 120 et 200. Le plus grand diviseur (facteur)
commun de 120 et de 200 est 40, d'où…
Puisque nous avons divisé le numérateur et le dénominateur par le même
nombre (40), la fraction 3 / 5 est équivalente à 120 / 200.
De plus 3 / 5 est la forme simplifiée de 120 / 200 puisque aucun
facteur commun n'existe pour 3 et 5. Une simplification peut s'effectuer en plusieurs étapes si on ne reconnaît
pas, à prime abord, le plus grand facteur commun du numérateur et du dénominateur.
Exemple
Les amateurs du "Compte est bon" auront remarqué que 108 et 144 avaient
pour facteur commun le nombre 36 :
Au bout du compte, quel que soit le nombre d'étapes effectuées, la même forme simplifiée sera trouvée… Règle d'addition et soustraction de fractions
Le symbole ± , qui se lit "plus ou moins", indique
que cette règle s'applique aussi bien aux additions qu'aux soustractions.
Exemple
Remarquez que la règle d'addition et de soustraction des fractions n'est
applicable que si les deux fractions possèdent le même dénominateur. Or,
ceci ne sera généralement pas le cas. Il faudra alors créer réécrire les
fractions en fractions équivalentes ayant un dénominateur commun.
Exemple évaluer la somme 2 / 5 + 1 / 3. Ces fractions ne peuvent être additionnées avant de les avoir réécrites avec un dénominateur commun. Le plus petit commun multiple des nombres 3 et 5 est 15… 15 sera donc le commun dénominateur.
Exemple évaluer la soustraction 3 / 8 - 17 / 24. Le dénominateur commun (le plus petit commun multiple) des nombres 8
et 24 est 24. La fraction
Remarque Il peut s'avérer utile d'effectuer, si possible, une simplification des
fractions avant de procéder à l'addition ou la soustraction. Une telle
simplification rendra plus facile l'obtention d'un dénominateur commun.
Exemple évaluer la somme 9 / 12 + 7 / 14
Dans l'exemple précédent, le dénominateur commun de 12 et 14 aurait été 84. En simplifiant d'abord chacune des fractions, les calculs ont été grandement réduits. Règle de multiplication de deux fractions
Il est important de noter que, contrairement aux additions, la règle
de multiplication n'impose aucune contrainte à la valeur des dénominateurs…
C'est-à-dire que ceux-ci n'ont nul besoin d'être communs. Exemple
Remarque Il peut être utile d'effectuer une simplification des fractions avant
de procéder à la multiplication. En plus de pouvoir simplifier chaque
fraction prise individuellement, simplifier le dénominateur d'une fraction
avec le numérateur de l'autre est permis pourvu que tous deux possèdent
des facteurs communs. Exemple évaluer le produit Vous remarquerez que les deux fractions en jeu, 27 / 16 et 8 / 81, sont
déjà exprimées sous forme simplifiée. Toutefois, le dénominateur 16 et
le numérateur 8 ont pour facteur commun le nombre 8. De plus, le dénominateur
81 et le numérateur 27 ont pour facteur commun le nombre 27. Il existe
donc quelques simplifications possibles avant d'effectuer le produit :
Règle de division de deux fractions
La règle permet donc de transformer une division de fraction en une multiplication.
Exemple
Attention à la notation suivante qui décrit la même division :
Quelques remarques finales
Exercices - Opérations sur les nombres Question 1 Effectuer les calculs suivants en respectant la priorité des opérations :
|



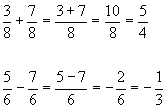
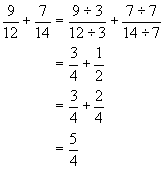
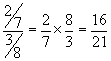 .
.